209x Filetype PDF File size 0.35 MB Source: isip.piconepress.com
IEEE Xtreme Programming Challenge tuf02749@temple.edu
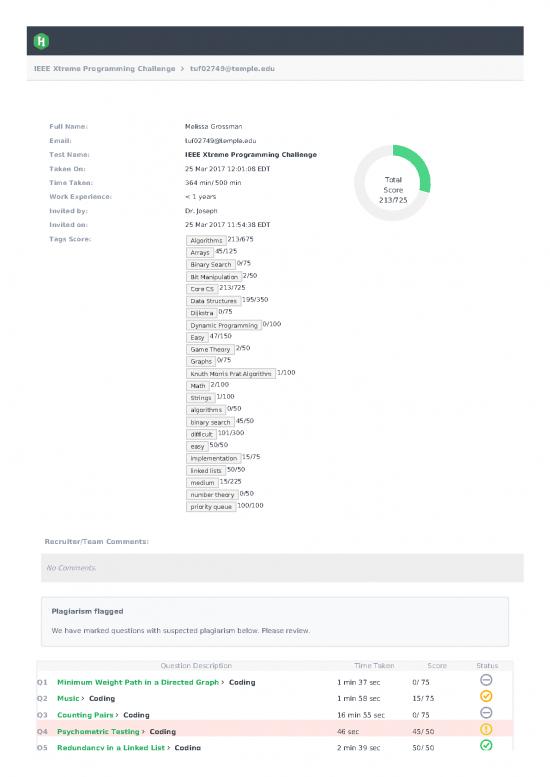
Full Name: Melissa Grossman
Email: tuf02749@temple.edu
Test Name: IEEE Xtreme Programming Challenge
Taken On: 25 Mar 2017 12:01:08 EDT
Total
Time Taken: 364 min/ 500 min
Score
Work Experience: < 1 years
213/725
Invited by: Dr. Joseph
Invited on: 25 Mar 2017 11:54:38 EDT
Tags Score: 213/675
Algorithms
45/125
Arrays
0/75
Binary Search
2/50
Bit Manipulation
213/725
Core CS
195/350
Data Structures
0/75
Dijkstra
0/100
Dynamic Programming
47/150
Easy
2/50
Game Theory
0/75
Graphs
1/100
Knuth Morris Prat Algorithm
2/100
Math
1/100
Strings
0/50
algorithms
45/50
binary search
101/300
difficult
50/50
easy
15/75
implementation
50/50
linked lists
15/225
medium
0/50
number theory
100/100
priority queue
Recruiter/Team Comments:
No Comments.
Plagiarism flagged
We have marked questions with suspected plagiarism below. Please review.
Question Description Time Taken Score Status
Q1 Minimum Weight Path in a Directed Graph Coding 1 min 37 sec 0/ 75
Q2 Music Coding 1 min 58 sec 15/ 75
Q3 Counting Pairs Coding 16 min 55 sec 0/ 75
Q4 Psychometric Testing Coding 46 sec 45/ 50
Q5 Redundancy in a Linked List Coding 2 min 39 sec 50/ 50
Q5 Redundancy in a Linked List Coding 2 min 39 sec 50/ 50
Question Description Time Taken Score Status
Q6 Sherlock and GCD Coding 7 min 54 sec 0/ 50
Q7 Counter game Coding 1 hour 30 min 58 sec 2/ 50
Q8 Vaccination Clinics Coding 3 hour 27 min 19 sec 100/ 100
Q9 String Similarity Coding 14 min 56 sec 1/ 100
Q10 A Very Special Multiple Coding 13 min 59 sec 0/ 100
medium Core CS
Minimum Weight Path in a Directed Graph Coding
QUESTION 1
Algorithms Data Structures Graphs Dijkstra
Not Submitted
QUESTION DESCRIPTION
We define a directed graph, g, such that:
Score 0
The total number of nodes in the graph is g_nodes.
The nodes are numbered sequentially as 1, 2, 3, …, g_nodes.
The total number of edges in the graph is g_edges.
Each edge connects two distinct nodes (i.e., no edge connects a node to itself).
The weight of the edge connecting nodes g_from[i] and g_to[i] is g_weight[i].
The edge connecting nodes g_from[i] and g_to[i] is directed. In other words, it describes a
path only in the direction g_from[i] → g_to[i].
We define the weight of a path from node 1 to node g_nodes to be the sum of all edges
traversed on that path.
Complete the minCost function in the editor below. It has four parameters:
1. An integer, g_nodes, denoting the number of nodes in graph g.
2. An array of integers, g_from, where each g_from[i] denotes the starting (source) node of
th
the i directed edge in graph g.
th
3. An array of integers, g_to, where each g_to[i] denotes the ending (target) node of the i
directed edge in graph g.
th
4. An array of integers, g_weight, where each g_weight[i] denotes the weight of the i
directed edge in graph g.
You must find the path from node 1 to node g_nodes having the minimum possible weight. You
can add extra directed edges having weight 1 (one) between any two distinct nodes that are
not already connected by an edge. The function must return an integer denoting the minimum
possible weight of any path from node 1 to node g_nodes.
Input Format
Locked stub code in the editor reads the following input from stdin and passes it to the
function:
The first line contains two space-separated integers describing the respective values of
g_nodes and g_edges.
Each line i of the g_edges subsequent lines contains three space-separated integers describing
the respective values of g_from[i], g_to[i], and g_weight[i].
Constraints
3
3 ≤ g_nodes ≤ 10
4 (g_nodes × (g_nodes − 1))
1 ≤ g_edges ≤ min(10 , ⁄ )
2
6
1 ≤ g_weight[i] ≤ 10
Output Format
The function must return an integer denoting the minimum weight of any possible path
(including one created by adding the optional additional directed edges) from node 1 to node
g_nodes. This is printed to stdout by locked stub code in the editor.
Sample Input 0
2 1
1 2 3
Sample Output 0
3
Explanation 0
A directed edge already exists from node 1 to node 2 and the path 1 → 2 is the minimum cost
A directed edge already exists from node 1 to node 2 and the path 1 → 2 is the minimum cost
path, so the function returns 3.
Sample Input 1
3 1
1 2 3
Sample Output 1
1
Explanation 1
As graph g has no edge between node 1 and node 3, we can add an extra edge from node1 to
node 3 having weight 1. Thus, the path 1 → 3 is the minimum weight path and the function
returns 1.
Sample Input 2
4 4
1 2 3
1 3 3
1 4 3
2 1 3
Sample Output 2
3
Explanation 2
A directed edge already exists from node 1 to node 4 and the path 1 → 4 is the minimum cost
path, so the function returns 3.
CANDIDATE ANSWER
No answer was submitted for this question. Showing compiled/saved versions.
Language used: C++
1 /*
2 * Complete the function below.
3 */
4 /*
5 For the weighted graph:
6 1. The number of nodes is _nodes.
7 2. The number of edges is _edges.
8 3. An edge exists between _from[i] to _to[i] and the weight of the edge is
9 _weight[i].
10 */
11 int minCost(int g_nodes, vector < int > g_from, vector < int > g_to, vector < int > g_weight) {
12
13
14 }
15
No Comments
medium Algorithms Core CS implementation
Music Coding
QUESTION 2
QUESTION DESCRIPTION
Correct Answer
Mark likes to listen to music while travelling. His iPod™ contains N songs and he wants to listen
to L (not necessarily different) songs during a trip. So he creates a playlist such that:
Score 15
Score 15
Every song is played at least once.
A song can be played again only if at least K other songs have been played
Mark wants to know how many different playlists are possible. Can you help Mark determine
this number? As the number can be very large, display number modulo 1,000,000,007.
You are given N, K and L. You have to complete the function with the following function
signature:
int numOfPlaylists(int N, int K, int L) {
}
Constraints
N lies between 1 and 100, inclusive.
K lies between 0 and N, inclusive.
L lies between N and 100, inclusive.
Sample Input #00:
1
0
3
Sample Output #00:
1
Explanation #00:
N = 1, so there is only 1 song in the iPod™. K = 0 so the song can be played as often as you
want. L = 3, and the only valid 3-song playlist is: {song_1, song_1, song_1}.
Sample Input #01:
1
1
3
Sample Output #01:
0
Explanation #01:
Again, there is only 1 song in the iPod™, but it cannot be played twice in a row because K = 1.
No valid playlists can be generated that are longer than l which is less than the requested L =
3.
CANDIDATE ANSWER
Language used: Python 2
1 # Complete the function below.
2
3
4 def numOfPlaylist( N, K, L):
5 c = 0;
6 if N > 100 or N < 0:
7 return 0
8 if K < 0 or K >= N:
9 return 0
10 if L < N or L > 100:
11 return 0
12 #for i in range(0,N):
13 # if i <= K:
14 #math.factorial(N)/math.factorial(K)
15 c=(nCr(N,K))*pow(N,(L-K))
16 # a=math.factorial(N-i)
17 # b = a * pow((N-K),(N-i))
18 #c +=b
19 return c % 1000000007
20
TESTCASE TYPE STATUS SCORE TIME TAKEN MEMORY USED
Testcase 0 Easy Runtime Error 0 0.01 sec 4.13 MB
Testcase 1 Easy Success 0 0.0 sec 4.78 MB
Testcase 2 Easy Runtime Error 0 0.01 sec 4.13 MB
Testcase 3 Easy Runtime Error 0 0.0 sec 4.13 MB
no reviews yet
Please Login to review.