206x Filetype PDF File size 1.62 MB Source: old.amu.ac.in
Unit – 3 (Response Surface Methodology)
3.1 Introduction: Response surface methodology (RSM) is a collection of mathematical and
statistical techniques useful for the modeling and analysis of problems in which a response of interest
is influenced by several variables and the objective is to optimize this response. For example,
suppose that a chemical engineer wishes to find the levels of temperature (x ) and pressure (x ) that
1 2
maximize the yield (y) of a process. The process yield is a function of the levels of temperature and
pressure, say
Y = f(x , x ) + error
1 2
where error represents the noise or error observed in the response y. If we denote the expected
response by E(y) = f(x , x ) = ɳ, then the surface represented by
1 2
ɳ = f(x , x )
1 2
is called a response surface.
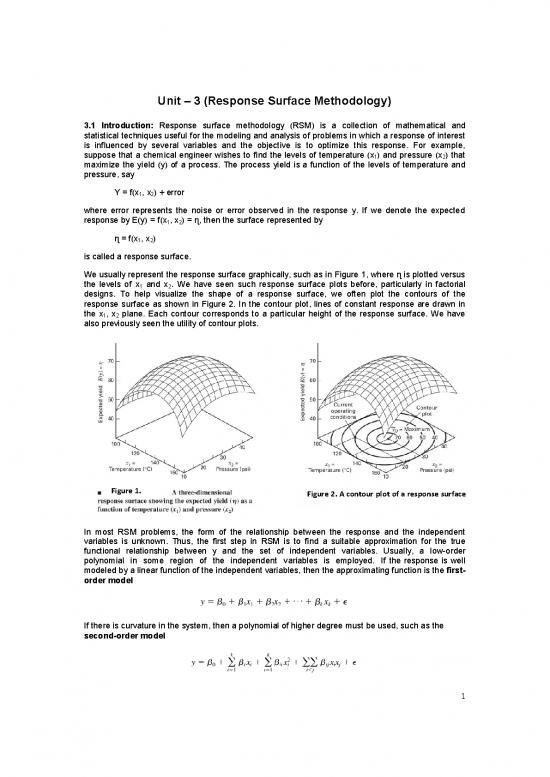
We usually represent the response surface graphically, such as in Figure 1, where ɳ is plotted versus
the levels of x and x . We have seen such response surface plots before, particularly in factorial
1 2
designs. To help visualize the shape of a response surface, we often plot the contours of the
response surface as shown in Figure 2. In the contour plot, lines of constant response are drawn in
the x , x plane. Each contour corresponds to a particular height of the response surface. We have
1 2
also previously seen the utility of contour plots.
Figure 1. Figure 2. A contour plot of a response surface
In most RSM problems, the form of the relationship between the response and the independent
variables is unknown. Thus, the first step in RSM is to find a suitable approximation for the true
functional relationship between y and the set of independent variables. Usually, a low-order
polynomial in some region of the independent variables is employed. If the response is well
modeled by a linear function of the independent variables, then the approximating function is the first-
order model
If there is curvature in the system, then a polynomial of higher degree must be used, such as the
second-order model
1
Designs for First-order Model Designs for Second-order Model
1. 2k full or fractional factorial design 1. 3k full or fractional factorial design
2. Plackett Burman design 2. Box-Behnken Design (BBD)
3. Simplex design 3. Central Composite Design (CCD
3.2 Advantages of Regression Method: Regression methods are extremely useful when something
“goes wrong” in a designed experiment. This is illustrated in the next two examples.
3
Example 1: A 2 Factorial Design with a Missing Observation
A chemical engineer is investigating the yield of a process. Three process variables are of interest:
temperature, pressure, and catalyst concentration. Each variable can be run at a low and a high
level, and the engineer decides to run a 23 design with four center points. The design and the
resulting yields are shown in Figure 3, where we have shown both the natural levels of the design
factor and the 1, +1 coded variable notation normally employed in 2k factorial designs to represent
the factor levels.
Figure 3
The fitted regression model is
Suppose that when this experiment was performed, the run 8 (run with all variables at the high
level) in Figure 3 was missing. This can happen for a variety of reasons; the measurement system can
produce a faulty reading, the combination of factor levels may prove infeasible, the experimental
unit may be damaged, and so forth. Therefore, the fitted model (using the remaining 11 runs) is
Compare this model to the one obtained where all 12 observations were used. The regression
coefficients are very similar. Because the regression coefficients are closely related to the factor
effects, our conclusions would not be seriously affected by the missing observation. However, note
that the design with missing value is no more orthogonal for effect estimators. Furthermore, the
variances of the regression coefficients are larger than they were in the original orthogonal design
with no missing data.
Example 2. Inaccurate Levels in Design Factors
When running a designed experiment, it is sometimes difficult to reach and hold the precise factor
levels required by the design. Small discrepancies are not important, but large ones are potentially of
2
more concern. Regression methods are useful in the analysis of a designed experiment where the
experimenter has been unable to obtain the required factor levels.
To illustrate, the experiment presented in Table 1 shows a variation of the 23 design from Example 1,
where many of the test combinations are not exactly the ones specified in the design. Most of the
difficulty seems to have occurred with the temperature variable.
Table 1. Experimental design for the problem in Example 1
The fitted regression model, with the coefficients reported to two decimal places, is
Comparing this to the original model in Example 1, where the factor levels were exactly those
specified by the design, we note very little difference. The practical interpretation of the results of
this experiment would not be seriously affected by the inability of the experimenter to achieve the
desired factor levels exactly.
Example 3. De-aliasing Interactions in a Fractional Factorial (not discussed here)
2 2 2
3.3 Meaning of R & Adjusted-R : The Table 1 reports the coefficient of multiple determination R ,
where
2
In designed experiments, R is a measure of the amount of reduction in the variability of y obtained by
using the regressor variables x , x , . . . , x in the model. However, it should be noted that a large
2 1 2 k
value of R does not necessarily imply that the regression model is a good one. Adding a variable to
2
the model will always increase R , regardless of whether the additional variable is statistically
significant or not. Thus, it is possible for models that have large values of R2 to yield poor predictions
of new observations or estimates of the mean response.
2
Because R always increases as we add terms to the model, some regression model builders prefer
2
to use an adjusted-R defined as
where (n – 1) and (n – p) are the total degree of freedoms (if n is the total number of runs)
and the degree of freedom associated with error, respectively.
3
2
In general, the adjusted-R statistic will not always increase as variables are added to the model. In
fact, if unnecessary terms are added, the value of R2 will often decrease. For example, consider the
2 adj 2
viscosity regression model. The R and the adjusted-R for the model is shown in Table 1. It is
computed as
2
R = 1 – (3479 / 47636) = 0.927 or 92.7%
2 2
R = {1 – (15 / 13) } (1 – 0.927 ) = 0.916 or 91.6%
adj
2 2 2
which is very close to the ordinary R . When R and R adj differ dramatically, there is a good chance
that non-significant terms have been included in the model.
Table 1. Minitab output for the viscosity regression model
2
PRESS (PRedicted Error Sum of Square) value and R : To calculate PRESS, we select an
Prediction
observation—for example, i. Fitting the regression model to the observation number i and thus
denoting the predicted value as ŷ. We may find the prediction error for observation i as e = y – ŷ.
i (i) i i
Similarly, the prediction error is calculated for all the remaining observations. Then the PRESS
statistic is defined as
2
Finally, we note that PRESS can be used to compute an approximate R for prediction, say
This statistic gives some indication of the predictive capability of the regression model. For the
viscosity regression model in Table 1, the value of the computed PRESS residuals is 5207.7. Then
4
no reviews yet
Please Login to review.