162x Filetype PDF File size 0.38 MB Source: research.google.com
Learning Binary Codes for High-Dimensional Data Using Bilinear Projections
Yunchao Gong Sanjiv Kumar HenryA.Rowley Svetlana Lazebnik
UNCChapelHill Google Research Google Research University of Illinois
yunchao@cs.unc.edu sanjivk@google.com har@google.com slazebni@illinois.edu
5
10
1
ITQ (feasible)
Abstract ITQ
ITQ (unfeasible)
Proposed
Proposed
0.8
Recent advances in visual recognition indicate that to 3
10
achievegoodretrievalandclassificationaccuracyonlarge- 0.6
scale datasets like ImageNet, extremely high-dimensional 1
10
visual descriptors, e.g., Fisher Vectors, are needed. We Recall@500.4
memory (MB) for projections
present a novel method for converting such descriptors to 0.2
−1
compact similarity-preserving binary codes that exploits 10
0
16 64 256 1000 4000 16000 64000
16 64 256 1000 4000 16000 64000
their natural matrix structure to reduce their dimensional- code size
code size
ity using compact bilinear projections instead of a single (a) NN search recall. (b) Storage requirements.
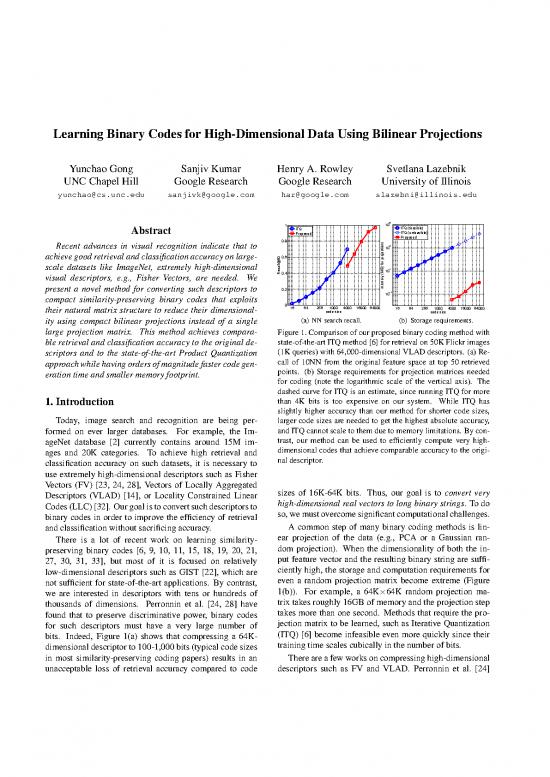
large projection matrix. This method achieves compara- Figure 1. Comparison of our proposed binary coding method with
ble retrieval and classification accuracy to the original de- state-of-the-art ITQ method [6] for retrieval on 50K Flickr images
scriptors and to the state-of-the-art Product Quantization (1Kqueries) with 64,000-dimensional VLAD descriptors. (a) Re-
approachwhilehavingordersofmagnitudefastercodegen- call of 10NN from the original feature space at top 50 retrieved
eration time and smaller memory footprint. points. (b) Storage requirements for projection matrices needed
for coding (note the logarithmic scale of the vertical axis). The
dashed curve for ITQ is an estimate, since running ITQ for more
1. Introduction than 4K bits is too expensive on our system. While ITQ has
slightly higher accuracy than our method for shorter code sizes,
Today, image search and recognition are being per- larger code sizes are needed to get the highest absolute accuracy,
formed on ever larger databases. For example, the Im- and ITQ cannot scale to them due to memory limitations. By con-
ageNet database [2] currently contains around 15M im- trast, our method can be used to efficiently compute very high-
ages and 20K categories. To achieve high retrieval and dimensional codes that achieve comparable accuracy to the origi-
classification accuracy on such datasets, it is necessary to nal descriptor.
use extremely high-dimensional descriptors such as Fisher
Vectors (FV) [23, 24, 28], Vectors of Locally Aggregated sizes of 16K-64K bits. Thus, our goal is to convert very
Descriptors (VLAD) [14], or Locality Constrained Linear high-dimensional real vectors to long binary strings. To do
Codes(LLC)[32]. Ourgoalistoconvertsuchdescriptorsto so, wemustovercomesignificantcomputationalchallenges.
binary codes in order to improve the efficiency of retrieval
and classification without sacrificing accuracy. Acommon step of many binary coding methods is lin-
There is a lot of recent work on learning similarity- ear projection of the data (e.g., PCA or a Gaussian ran-
preserving binary codes [6, 9, 10, 11, 15, 18, 19, 20, 21, dom projection). When the dimensionality of both the in-
27, 30, 31, 33], but most of it is focused on relatively put feature vector and the resulting binary string are suffi-
low-dimensional descriptors such as GIST [22], which are ciently high, the storage and computation requirements for
not sufficient for state-of-the-art applications. By contrast, even a random projection matrix become extreme (Figure
we are interested in descriptors with tens or hundreds of 1(b)). For example, a 64K×64K random projection ma-
thousands of dimensions. Perronnin et al. [24, 28] have trix takes roughly 16GB of memory and the projection step
found that to preserve discriminative power, binary codes takes more than one second. Methods that require the pro-
for such descriptors must have a very large number of jection matrix to be learned, such as Iterative Quantization
bits. Indeed, Figure 1(a) shows that compressing a 64K- (ITQ) [6] become infeasible even more quickly since their
dimensional descriptor to 100-1,000 bits (typical code sizes training time scales cubically in the number of bits.
in most similarity-preserving coding papers) results in an Thereareafewworksoncompressinghigh-dimensional
unacceptable loss of retrieval accuracy compared to code descriptors such as FV and VLAD. Perronnin et al. [24]
have investigated a few basic methods including thresh- 2.1. Random Bilinear Binary Codes
olding, Locality Sensitive Hashing (LSH) [1], and Spec- To convert a descriptor x ∈ Rd to a d-dimensional bi-
tral Hashing (SH) [33]. A more powerful method, Prod- nary string, we first consider the framework of [1, 6] that
uct Quantization (PQ) [13], has produced state-of-the-art applies a random rotation R ∈ Rd×d to x:
results for compressing FV for large-scale image classifica-
tion [28]. However, descriptors like FV and VLAD require
arandomrotationtobalancetheirvariancepriortoPQ[14], H(x)=sgn(RTx). (2)
and as explained above, rotation becomes quite expensive
for high dimensions. Since x can be represented as a matrix X ∈ Rd1×d2, to
In this paper, we propose a bilinear method that takes make rotation more efficient, we propose a bilinear formu-
advantage of the natural two-dimensional structure of de- lation using two random orthogonal matrices R1 ∈ Rd1×d1
scriptors such as FV, VLAD, and LLC and uses two smaller and R2 ∈ Rd2×d2:
matrices to implicitly represent one big rotation or projec-
tion matrix. Thismethodisinspiredbybilinearmodelsused H(X)=vec sgn(RTXR ) , (3)
for other applications [26, 29, 34]. We begin with a method 1 2
based on random bilinear projections and then show how to
efficiently learn the projections from data. We demonstrate where vec(·) denotes column-wise concatenation.
the promise of our method, dubbed bilinear projection- It is easy to show that applying a bilinear rotation to X ∈
d ×d
based binary codes (BPBC), through experiments on two R 1 2 is equivalent to applying a d d × d d rotation to
1 2 1 2
ˆ
large-scale datasets and two descriptors, VLAD and LLC. vec(X). This rotation is given by R = R ⊗ R , where ⊗
2 1
For most scenarios we consider, BPBC produces little or no denotes the Kronecker product:
degradation in performance compared to the original con-
tinuous descriptors; furthermore, it matches the accuracy of T T T ˆT
vec(R XR2)=(R ⊗R )vec(X)=R vec(X)
PQcodes while having much lower running time and stor- 1 2 1
age requirements for code generation. follows from the properties of the Kronecker product [16].
2. Bilinear Binary Codes Another basic property of the Kronecker product is that if
R and R are orthogonal, then R ⊗ R is orthogonal as
1 2 2 1
Mosthigh-dimensionaldescriptors have a natural matrix well [16]. Thus, a bilinear rotation is simply a special case
ˆ
or tensor structure. For example, a HOG descriptor is a of a full rotation, such that the full rotation matrix R can be
reconstructed from two smaller matrices R and R .
two-dimensional grid of histograms, and this structure has 1 2
been exploited for object detection [26]. A Fisher Vector While the degree of freedom of our bilinear rotation is
can be represented as a k × 2l matrix, where k is the visual more restricted than a full rotation, the projection matri-
vocabulary size and l is the dimensionality of the local im- ces are much smaller, and the projection speed is much
age features (the most common choice is SIFT with l=128). faster. In terms of time complexity, performing a full ro-
tation on x takes O((d d )2) time, while our approach is
VLAD,whichcanbeseenasasimplifiedversionofFV,can 1 2
2 2
O(d d + d d ). In terms of space for projections, full
berepresented as a k×l matrix. Finally, an LLC descriptor 1 2 1 2
rotation takes O((d d )2), and our approach only takes
with s spatial bins can be represented as a k × s matrix. 1 2
2 2
O(d + d ). For example, as will be shown in Section
Let x ∈ Rd denote our descriptor vector. Based on the 1 2
structureandinterpretationofthedescriptor,1 wereorganize 3.4, for a 64K-dimensional vector, a full rotation will take
it into a d × d matrix with d = d d : roughly 16GB of RAM, while the bilinear rotations only
1 2 1 2 take 1MBofRAM.Theprojectiontimeforafullrotationis
d d ×1 d ×d morethanasecond, vs. only 3 ms for bilinear rotations.
x∈R1 2 7→ X ∈R 1 2. (1)
We assume that each vector x ∈ Rd is zero-centered and 2.2. Learning Bilinear Binary Codes
has unit norm, as L normalization is a widely used prepro-
2 In this section, we present a method for learning the ro-
cessing step that usually improves performance [25]. tations R and R that is inspired by two-sided Procrustes
We will first introduce a randomized method to obtain 1 2
d-bit bilinear codes in Section 2.1 and then explain how analysis [29] and builds on our earlier work [5, 6, 7].
ˆ
to learn data-dependent codes in Section 2.2. Learning of Following [6], we want to find a rotation R such that
ˆT
the angle θ between a rotated feature vector R x =
reduced-dimension codes will be discussed in Section 2.3. i i
vec(RTX R ) and its binary encoding (geometrically, the
1 i 2
1 ˆT
We have also tried to randomly reorganize descriptors into matrices nearest vertex of the binary hypercube), sgn(R x) =
but found it to produce inferior performance. vec(sgn(RTX R )), is minimized. Given N training
1 i 2
0.02
0.05
0.015
0.04
0.01
0.03
0.005
0.02
0
0.01
−0.005
0
SIFT dimension −0.01
SIFT dimensions −0.01 SIFT dimensions SIFT dimensions
−0.015
−0.02
−0.02
−0.03
−0.025
visual codewords
visual codewords visual codewords visual codewords
(a) Original VLAD descriptor (b) Original binary code (c) Bilinearly rotated VLAD (d) Bilinearly rotated binary code
Figure 2. Visualization of the VLAD descriptor and resulting binary code (given by the sign function) before and after learned bilinear
rotation. We only show the first 32 SIFT dimensions and visual codewords. Before the rotation, we can clearly see a block pattern, with
manyzerovalues. After the rotation, the descriptor and the binary code look more whitened.
P
points, we want to maximize where D = N (B RTXT). The above expression is
1 i=1 i 2 i
X maximized with the help of polar decomposition: R1 =
N V UT,whereD =U S VT istheSVDofD .
cos(θ ) 1 1 1 1 1
i=1 i 1 1
X ˆT T ! (S3) Update R2:
N sgn(R xi) ˆT
= i=1 √ (R xi) (4) X
d N T T
Q(R ) = tr(B R X R )
X T T 2 i=1 i 2 i 1
N vec(sgn(R X R ))
1 i 2 T X
= √ vec(R X R ) N
i=1 1 i 2 = tr(RTXTR B )
d i=1 2 i 1 i
X �
1 N X
√ T T T N T T
= vec(B ) vec(R X R )
i 1 i 2 = tr R (X R B ) =tr(R D ),
d i=1 2 i=1 i 1 i 2 2
X
1 N T T P
= √ tr(B R X R ), (5) N T
i 2 i 1 where D = (X R B ). Analogously to the update
d i=1 2 i=1 i 1 i
rule for R , the update rule for R is R = U V T, where
1 2 2 2 2
where B = sgn(RTX R ). Notice that (4) involves the D =U S VT istheSVDofD .
i 1 i 2 2 2 2 2 2
ˆ d×d
large projection matrix R ∈ R , direct optimization of Wecycle between these updates for several iterations to
which is challenging. However, after reformulation into bi- obtainalocalmaximum. Theconvergenceoftheabovepro-
linear form (5), the expression only involves the two small gram is guaranteed in finite number of iterations as the op-
matrices R and R . Letting B = {B ,...,B }, our ob-
1 2 1 N timal solution of each step is exactly obtained, each step
jective function is as follows: is guaranteed not to decrease the objective function value,
N and the objective function is bounded from above. In our
Q(B,R ,R )= max Xtr(B RTXTR ) (6) implementation, we initialize R1 and R2 by random rota-
1 2 B,R ,R i 2 i 1
1 2 i=1 tions and use three iterations. We have not found significant
d ×d T T improvement of performance by using more iterations. The
s.t. B ∈ {−1,+1} 1 2, R R =I, R R =I.
i 1 1 2 2 3 3
timecomplexityofthisprogramisO(N(d +d ))whered1
1 2
This optimization problem can be solved by block coordi- andd aretypicallyfairlysmall(e.g.,d = 128, d = 500).
2 1 2
nate ascent by alternating between the different variables Figure 2 visualizes the structure of a VLAD descrip-
{B ,...,B }, R , and R . We describe the update steps tor and the corresponding binary code before and after a
1 N 1 2
for each variable below, assuming the others are fixed. learned bilinear rotation.
(S1) Update Bi. When R1 and R2 are fixed, we indepen- 2.3. Learning with Dimensionality Reduction
dently solve for each B by maximizing
i
P P The formulation of Section 2.2 is used to learn d-
T T d1 d2 kl elk
Q(B ) = tr(B R X R ) = B V ,
i i 2 i 1 k=1 l=1 i i dimensional binary codes starting from d-dimensional de-
elk e T T scriptors. Now, to produce a code of size c = c1 × c2,
where V denote the elements of V = R X R . Q(B )
i i 2 i 1 i where c1 < d1 and c2 < d2, we need projection matrices
eT d ×c d ×c T
is maximized by Bi = sgn(Vi ). R ∈ R 1 1, R ∈ R 2 2 such that R R = I and
1 2 1 1
(S2) Update R . Expanding (6) with R and B fixed, we RTR =I.EachB isnowac ×c binaryvariable. Con-
1 2 i 2 2 i 1 2
have the following: sider the cosine of the angle between a lower-dimensional
ˆT ˆT
XN projected vector R xi and its binary encoding sgn(R x):
Q(R ) = tr(B RTXTR )
1 i=1 i 2 i 1
ˆT T ˆT
sgn(R x ) R xi
X i
N T T cos(θ ) = √ ,
= tr (B R X )R =tr(D R ), i ˆT
i 2 i 1 1 1 c kR x k
i=1 i 2
d d ×c c T
ˆ 1 2 1 2 ˆ ˆ
where R ∈ R and R R = I. This formulation The second dataset is the ILSVRC2010 subset of Ima-
ˆT
differs from that of (4) in that it contains kR x k in the geNet [2], which contains 1.2M images and 1,000 classes.
i 2
denominator,whichmakestheoptimizationdifficult[5]. In- Onthisdataset, weusethepubliclyavailableSIFTfeatures,
stead, we follow [5] to define a relaxed objective function which are densely extracted from the images at three dif-
based on the sum of linear correlations ferent scales. We cluster the features into 200 centers and
X ˆT T ! then aggregate them into VLAD vectors of 128 × 200 =
N sgn(R xi) ˆT 25,600 dimensions. These vectors are also power- and L -
Q(B,R ,R )= √ (R x ) . 2
1 2 i=1 c i normalized. In addition, we compute LLC features [32] on
The optimization framework for this objective is similar to this dataset using a 5,000-dimensional visual codebook and
that of Section 2.2. For the three alternating optimization athree-level spatial pyramid (21 spatial bins). The resulting
steps, (S1) remains the same. For (S2) and (S3), we com- features have 5,000 × 21 = 105,000 dimensions. Unlike
pute the SVD of D and D as U S VT and U S VT re- VLADdescriptors, which are dense and have both positive
1 2 1 1 1 2 2 2 and negative values, the LLC descriptors are nonnegative
ˆ T and
spectively, and set the two rotations to R = V U
1 1 1 and sparse. For improved results, we zero-center and L -
ˆ T ˆ 2
R =U V ,whereV isthetopc singular vectors of V
2 2 2 1 1 1 normalize them.
ˆ
and U is the top c singular vectors of U . To initialize the
2 2 2
optimization, we generate random orthogonal directions. 3.2. Experimental Protocols
2.4. Distance Computation for Binary Codes To learn binary codes using the methods of Sections 2.2
At retrieval time, given a query descriptor, we need to and 2.3, we randomly sample 20,000 training images from
compute its distance to every binary code in the database. each dataset. We then set aside a number of query images
The most popular measure of distance for binary codes is that were not used for training and run nearest neighbor
the Hammingdistance. Wecomputeitefficientlybyputting searches against all the other images in the dataset. For
bits in groups of 64 and performing an XOR and bit count Holiday+Flickr1M, we sample the training images from
(popcount). Forimprovedaccuracy,weuseasymmetricdis- the Flickr subset only and use the 500 predefined queries.
tance, in which the database points are quantized but the For ILSVRC2010, we use 1,000 random queries. For each
query is not [3, 8, 13]. In this work, we adopt the lower- dataset, we evaluate two types of retrieval tasks:
bounded asymmetric distance proposed in [3] to measure 1. Retrieval of ground-truth nearest neighbors from the
the distance between the query and binary codes. For a original feature space. These are defined as the top
query x ∈ Rc and database points b ∈ {−1,+1}c, the ten Euclidean nearest neighbors for each query based
lower-bounded asymmetric distance is simply the L dis- on original descriptors. Our performance measure for
2
tance between x and b: d (x,b) = kxk2 + c − 2xTb. this task is the recall of 10NN for different numbers of
a 2
2
Since kxk is on the query side and c is fixed, in practice, retrieved points [9, 13].
2
T
we only need to compute x b. We do this by putting bits 2. Retrieval of “relevant” or “semantically correct”
in groups of 8 and constructing a 1 × 256 lookup table to neighbors. For Holiday+Flickr1M, these are defined
makethedot-product computation more efficient. as the images showing the same object instance (re-
3. Experiments call from Section 3.1 that each query has around
three matches). The standard performance measure
3.1. Datasets and Features for this task on this dataset is mean average precision
(mAP) [8, 12, 14]. For ILSVRC2010, we define the
Wetestourproposedapproach,bilinearprojection-based ground-truth “relevant” neighbors as the images shar-
binary codes (BPBC), on two large-scale image datasets ing the same category label. In this case, there are very
and two feature types. The first one is the INRIA Holiday many matches for each query. Following [6, 18, 20],
dataset with 1M Flickr distractors (Holiday+Flickr1M) we report performance using precision at top k re-
[12]. There are 1,419 images in the Holiday dataset cor- trieved images (precision@k).
responding to 500 different scene instances, and each in- In addition, in Section 3.8 we perform image classification
stance has three images on average. There is a set of 500 experiments on the ILSVRC2010 dataset.
query images, and the remaining 919 images together with
the 1M Flickr images are used as the database. We use the 3.3. Baseline Methods
SIFT features of interest points provided by [14] and clus-
ter them to 500 k-means centers. Then we represent each Our main baseline is the state-of-the-art Product Quan-
image by a 128 × 500 = 64,000 dimensional VLAD. The tization (PQ) approach [13]. PQ groups the data dimen-
vectors are power-normalized(element-wisesquare-rooted) sions in batches of size s and quantizes each group with k
and L2-normalized as in [25]. codebook centers. In our experiments, we use s = 8 and
no reviews yet
Please Login to review.