163x Filetype PDF File size 0.98 MB Source: people.utm.my
CHAPTER 1: FIRST ORDER ORDINARY DIFFERENTIAL EQUATION SSE1793
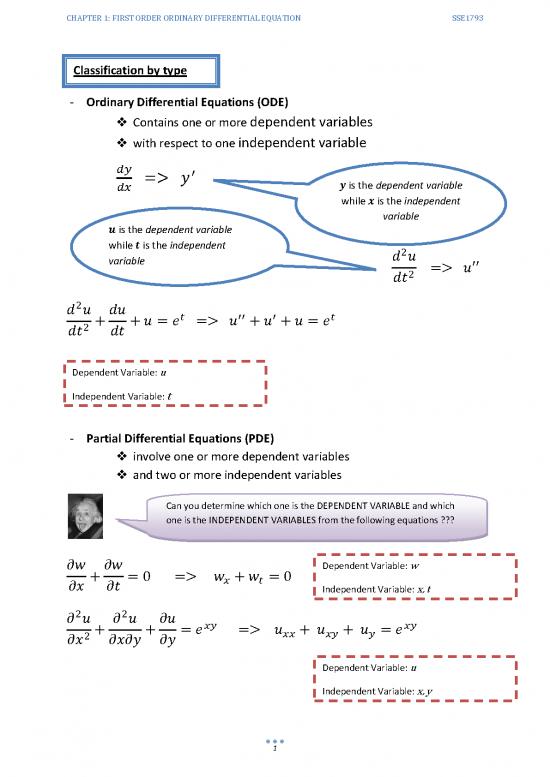
Classification by type
- Ordinary Differential Equations (ODE)
Contains one or more dependent variables
with respect to one independent variable
is the dependent variable
while is the independent
variable
is the dependent variable
while is the independent
variable
Dependent Variable: u
Independent Variable: t
- Partial Differential Equations (PDE)
involve one or more dependent variables
and two or more independent variables
Can you determine which one is the DEPENDENT VARIABLE and which
one is the INDEPENDENT VARIABLES from the following equations ???
Dependent Variable: w
Independent Variable: x, t
Dependent Variable: u
Independent Variable: x, y
1
CHAPTER 1: FIRST ORDER ORDINARY DIFFERENTIAL EQUATION SSE1793
Classification by order / degree
- Order of Differential Equation
Determined by the highest derivative
- Degree of Differential Equation
Exponent of the highest derivative
Examples:
Order : 1 Degree: 2
a)
b) Order : 2 Degree: 1
c) Order : 2 Degree: 1
d) Order : 3 Degree: 4
Classification as linear / nonlinear
- Linear Differential Equations
Dependent variables and their derivative are of degree 1
Each coefficient depends only on the independent variable
A DE is linear if it has the form
Examples:
1) 2)
3)
2
CHAPTER 1: FIRST ORDER ORDINARY DIFFERENTIAL EQUATION SSE1793
- Nonlinear Differential Equations
Dependent variables and their derivatives are not of degree 1
Examples:
1)
Order : 1 Degree: 1
2)
Order : 1 Degree: 2
3)
Order : 3 Degree: 2
Initial & Boundary Value Problems
Initial conditions : will be given on specified given point
Boundary conditions : will be given on some points
Examples :
1) Initial condition
2) Boundary condition
Initial Value Problems (IVP)
Initial Conditions:
Boundary Value Problems (BVP)
Boundary Conditions:
3
CHAPTER 1: FIRST ORDER ORDINARY DIFFERENTIAL EQUATION SSE1793
Solution of a Differential Equation
- General Solutions
Solution with arbitrary constant depending on the order
of the equation
- Particular Solutions
Solution that satisfies given boundary or initial conditions
Examples:
(1)
Show that the above equation is a solution of the following DE
(2)
Solutions:
(3)
(4)
Insert (1) and (4) into (2)
Proven that is the solution for the given DE.
EXERCISE:
Show that is the solution of the
following DE
4
no reviews yet
Please Login to review.