Filetype PDF | Posted on 27 Jan 2023 | 2 years ago
Authentication
digital resources
139x Filetype PDF File size 0.51 MB Source: www.mathcity.org
Notes of Chapter 02: Calculus with Analytic Geometry by Ilmi Kitab Khana, Lahore.
x
i
f 30 I
1
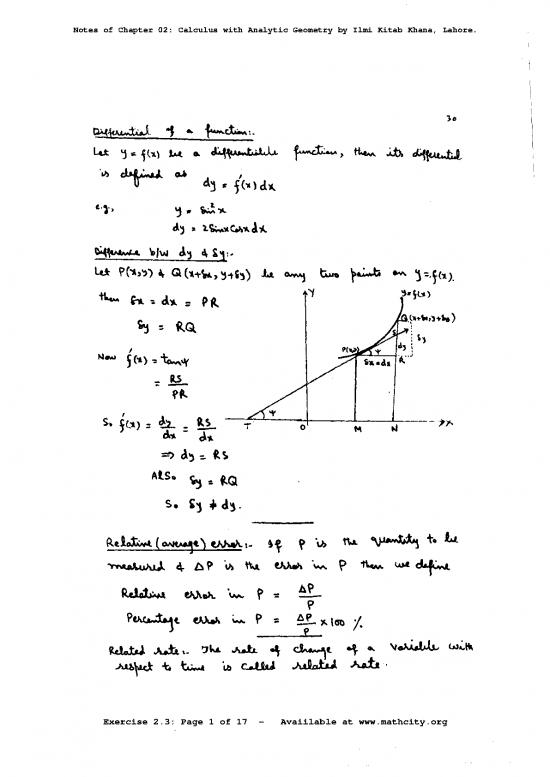
Lu: ‘j:-§(1)h-I. fw-¢1I:-~, M.11‘); 1
o.
'v> cu ,'
43 = fhidx
"1" ‘Jr
A5 = 7-$I~\xCwAA'L
hlw J3 481:-
Lii P(“l>‘)) §- G(‘l+§J.,f}-+93) -Ll. Qmaj but NA '3:,S.(1)_
11... 5,.‘ 3 ‘M PK T‘! ~a=§m
$3 _$:\-V‘23+$Q )
1
I
o ‘>5
1 Pm» A3}
N“ 5(1) '= t>~\\¥ ss. Mn "3
= 5.2..
WK ‘
: __‘\’7
s.;@>=%=;<£. T’ 0- ~.,‘ ., ~~>>~
=')A§:.k§
AIS. Q3
S. S3 #43. -
i_le.\o1'»'»l.§ou0.p¢&1)U¢,.)\:‘_ 5% P -U, Th. ‘\)J0-IJ»5'\'~1~|.
-~w.wuA¢AP'v>m w»>.\~\Pw.w1d-f.'~¢
Puu.h1o.eAJ»aL~,.P= 9_?_x\on/_
__.____Y.._.
¢;_\,,j3}_;\_,h,- Uka. Jab. J; Ml ~§- °~ V¢’**l-Vb- "~’*-“\
M>\¢¢+.t.;... u,¢.ua».J.ox»\~h-
Exercise 2.3: Page 1 of 17 - Avaiilable at www.mathcity.org
Notes of Chapter 02: Calculus with Analytic Geometry by Ilmi Kitab Khana, Lahore.
._e\w:=n:uu~w...w,~--»>»=~ - - ~ -\.Pv'!&¢»'_-'—
---»».), -.. ., ~ ‘~>"4\I\r V
mm--v.. -V...‘ - .-
, ' . .1=m_.. ..=—...-\.
EXERCISE2.3
.
/'
Find‘Ay, dy, A)’ "dy if l
1.0) y =x“-1, x=1"~.% ~==-0-5
(u) Y = ===2. Ax=0-3'
301. ~ y = I3’
1) Here L(-0-5)
<55 = 3(\)
. A‘) = §(a+n)—S(-1)
,[(1+n)3-1] -[Q-J = 30“)
: (ii-Q-51),-4 -1‘+\ 2 ‘J8
3 Now
(‘+b‘) "3
= (\-<>.s)1-(U3 A\5""‘J * '°‘“5 ’("‘"'§)
(°.s)3_‘ 2 -O"-‘K
6-1 '.: 011$ __. Kw»
1'. 15-I
bu : -O-$75 -._
g 1;.-_-_~ ». ~_ .
$3 : 317TA'\l i
.. :: -3
(ii) y = ~11-3x-2 7 ‘-7-)5)‘ O
S&‘_ Q.‘
.-~*s-F5-1
A3 1 §(1+M.3-§-(M ‘I’ PM G)
‘,5 , _~,/__.=,.,.-1*
1571
~ = -“"I'**
\ 1 $31.1.
= ';(-its)-1 "Si" Q = _.'>_.__.<<»-3»
1
-Z -= _--—-"""
A3 .. O-'l\3§ Ag : O-Ilse
MUM?
z>~;_A~, = @-'z.\s§» 0-119°
g ~"""' 9w-5
Exercise 2.3: Page 2 of 17 - Avaiilable at www.mathcity.org
0‘
'."’.=-
-Q".
T\
"'0
LUO:
Notes of Chapter 02: Calculus with Analytic Geometry by Ilmi Kitab Khana, Lahore.
32.
2. Use di“f'erentials to -approxiamte
(i) V262 4'
Sol. We consider
y = rm = ~/I __~.......--__~.__~~__<1;
with x = 25 and Ax = 1.2
From (1), we have
- d = 1
“-* dx
_y 2~E ‘ - ' _____ A (2,
* -
Substituting x = 25, (1.; = Ax = 1.2 in (2), we get
A) -1 _.L—-.(\.7.)
25? _g ., O-\'L
.3.-(\-1)
1‘!-5 : ‘O-VI.-\~§
_ \-2.
—-":‘
= 0-\‘L
"‘°‘~‘ A3 ch A5 = f(1+z>1)-§(>\,)
A3 = -5-
V
on = $33 -XI;
0.\7_ -= ‘ll.-7. -5
(ii) V80.9
301- Let J’ = /'(r) = \/E Now A51: A~3=§(1+m)-§l_~1)
H-u1‘A=Q\ and Ax: -—O.1=zlx
A3 LA‘ A =§H -
5 1+A1 F'
2;? -0-005$! = JQ\..¢.\ - ET
I- —-——_ (L-o.\)
zri-‘ —o-ooS§§ =‘Qh-Q -q
.. -0-‘
= 2*‘ S30-W _-Q : -0-4>0§§$'
-6-\
W £30-'\ =, -0-0\'§S§+q
Exercise 2.3: Page 3 of 17 - Avaiilable at www.mathcity.org
s
~55];
Notes of Chapter 02: Calculus with Analytic Geometry by Ilmi Kitab Khana, Lahore.
3
i
s
§
i
|
'5; I‘
W
1»
1
'5‘
‘Q; at
-;\.<-'_»~ ~ 1
.
=~. ~ . . - r.v.l.\'\4.Ԥ-;
. _ . a
H.-5-,.» ._,...t M. »-. *1
(iii) “*1 123
Sol. ‘I; ‘*3 = - %;
‘I -0-O1‘-L
WM 15; 9 (V2.3) ‘
Lu 5=§(-n = {'3 -~~ A;-'.- A3: §(1-vmn-*§(~n
‘b"'z' \' ‘I
l-u;.\\ ~.\-¢\1-S J3 = ('a+m\)‘- x3
\ \ ‘I ‘I3
9'3"" A3 -: ‘$1.3- A‘ -o-oz“ -_-_ (I152-Z)’-(\1$)
1 Q '1 ‘I
.. .1.§"‘h = (my- (Q) ’
-¢..n.u,= I],
(n3) - $
\ ("7- | ‘
‘: ---—-1' 3 "_ =- . ct
MM), ‘ (na) S ¢>°1
-'1 V3 = -o-o'1(.(+§
-1 “"’ g
3(5)‘
(iv) cos 61' Jji bf) 1: $(‘\+A\)-_¥'(\\)
Ixtu = cos; Nan
- A‘) 14'-'o.'>((5+\. -C09‘.
“ma a.L2=¢-~».L=.!‘_- , ) O
Ho 3 _'§_-L : QM -'-L
Q :- 1~ ‘K '= L ‘ 3‘. 1
Q» A1 2 \ xu us»
(1-1 1 (1-\ 3
NM A3 ., _$~‘~.a ‘
=-%A(r1;\.-1%“ -o~\Sn. - QM“-¢-§
‘K G,Q\._t>~S -; -O-\§\L
.;,=- \B0 q (Z,,g\' = -O-\S\1+o~$
= o-‘\3‘1$
l 1%,.---1
Exercise 2.3: Page 4 of 17 - Avaiilable at www.mathcity.org
II
W
;;\'
0|
9-
ul-
J3‘
no reviews yet
Please Login to review.
