228x Filetype PDF File size 0.32 MB Source: www.mib.uni-stuttgart.de
Universit¨at Stuttgart Institut fu¨r Mechanik
Prof. Dr.-Ing. W. Ehlers
www.mechbau.uni-stuttgart.de
Vector and Tensor Calculus
An Introduction
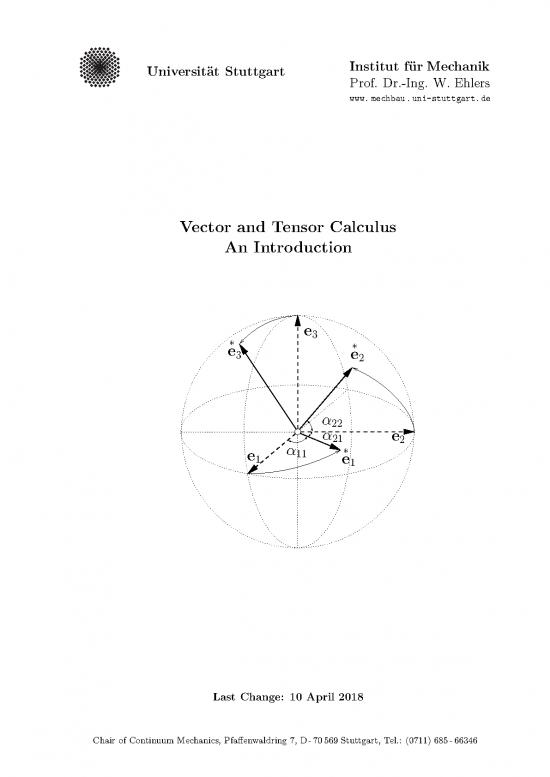
e3
∗ ∗
e3 e2
α
22
α e
21 2
α ∗
e1 11 e
1
Last Change: 10 April 2018
Chair of Continuum Mechanics, Pfaffenwaldring 7, D-70569 Stuttgart, Tel.: (0711) 685-66346
Contents
1 Mathematical Prerequisites 1
1.1 Basics of vector calculus . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
2 Fundamentals of tensor calculus 9
2.1 Introduction of the tensor concept . . . . . . . . . . . . . . . . . . . . . . . 9
2.2 Basic rules of tensor algebra . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.3 Specific tensors and operations . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.4 Change of the basis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.5 Higher order tensors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.6 Fundamental tensor of 3rd order (Ricci permutation tensor) . . . . . . . . 28
2.7 The axial vector . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.8 The outer tensor product of tensors . . . . . . . . . . . . . . . . . . . . . . 33
2.9 The eigenvalue problem and the invariants of tensors . . . . . . . . . . . . 34
3 Fundamentals of vector and tensor analysis 36
3.1 Introduction of functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
3.2 Functions of scalar variables . . . . . . . . . . . . . . . . . . . . . . . . . . 36
3.3 Functions of vector and tensor variables . . . . . . . . . . . . . . . . . . . . 37
3.4 Integral theorems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3.5 Transformations between actual and reference configurations . . . . . . . . 46
no reviews yet
Please Login to review.