158x Filetype PDF File size 0.05 MB Source: math.hawaii.edu
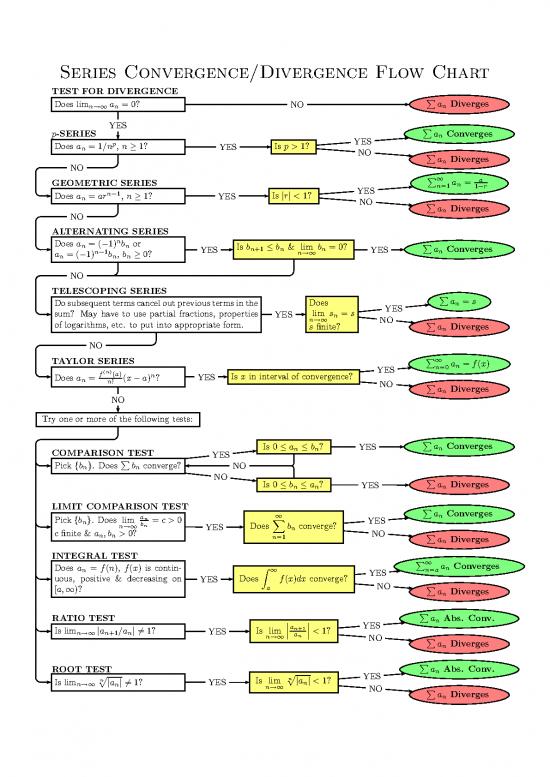
Series Convergence/Divergence Flow Chart
TEST FOR DIVERGENCE
Does lim a =0? NO Pan Diverges
n→∞ n
YES
p-SERIES p YES Pan Converges
Does an = 1=n , n ≥ 1? YES Is p > 1?
NO NO Pan Diverges
P
GEOMETRICSERIES ∞ a = a
n=1 n 1−r
Does a =arn−1, n ≥ 1? YES Is |r| < 1? YES
n
NO NO Pan Diverges
ALTERNATING SERIES
n
Does an = (−1) bn or YES Is bn+1 ≤ bn & lim bn = 0? YES Pan Converges
n−1 n→∞
an = (−1) bn, bn ≥ 0?
NO
TELESCOPING SERIES
Dosubsequenttermscanceloutprevioustermsinthe Does YES Pan=s
sum? May have to use partial fractions, properties YES lim sn = s
n→∞
of logarithms, etc. to put into appropriate form. s finite? NO Pan Diverges
NO
P
TAYLORSERIES ∞ a =f(x)
YES n=0 n
f(n)(a) n YES Is x in interval of convergence?
Does an = n! (x−a) ? NO Pa Diverges
n
NO
Try one or more of the following tests:
COMPARISONTEST YES Is 0 ≤ an ≤ bn? YES Pan Converges
Pick {bn}. Does Pbn converge? NO NO
Is 0 ≤ bn ≤ an? YES Pan Diverges
LIMIT COMPARISON TEST
a ∞ Pan Converges
n
Pick {bn}. Does lim b = c > 0 X YES
n→∞ n YES Does bn converge?
c finite & an;bn > 0? n=1 NO Pan Diverges
INTEGRALTEST
P
∞ a Converges
Does an = f(n), f(x) is contin- Z ∞ YES n=a n
uous, positive & decreasing on YES Does f(x)dx converge?
[a;∞)? a NO Pan Diverges
RATIO TEST
YES Pan Abs. Conv.
a
Is lim |a =a | 6= 1? Is lim n+1 <1?
n→∞ n+1 n YES
a
n→∞ n
NO Pan Diverges
ROOTTEST p Pan Abs. Conv.
p n YES
Is lim n |a | 6= 1? YES Is lim |an| < 1?
n→∞ n n→∞
NO Pan Diverges
Problems 1-38 from Stewart’s Calculus, page 784
∞ 2 ∞ ∞
1. X n −1 14. Xsin(n) 27. X kln(k)
2 3
n=1 n +n n=1 k=1 (k +1)
∞ ∞
Xn−1 X n! ∞ 1=n
2. n2 +n 15. 2·5·8·····(3n+2) 28. Xe 2
n=1 n=0 n=1 n
∞ ∞ 2
X 1 Xn +1 ∞ −1
3. n=1 n2 +n 16. n=1 n3 +1 29. Xtan√(n)
n=1 n n
∞ ∞
X n−1n−1 X n1=n ∞ √
4. (−1) n2 +n 17. (−1) 2 X j j
n=1 n=1 30. (−1) j +5
j=1
∞ n+1 ∞ n−1
X(−3) X(−1)
5. 3n 18. √ ∞ k
n=1 2 n=2 n−1 31. X k5 k
3 +4
∞ ∞
n k=1
X 3n X nln(n)
6. 1+8n 19. (−1) √ ∞
n n
n=1 n=1 32. X(2n)
n2n
∞ ∞
7. X p1 20. Xk+5 n=1
n ln(n) 5k
∞
n=2 k=1 Xsin(1=n)
∞ k ∞ 33. √
X 2n n
8. 2 k! 21. X (−2) n=1
(k +2)! nn
k=1 n=1 ∞
∞ ∞ √ 34. X 1 2
9. Xk2e−k 22. X n2 −1 n=1 n+ncos (n)
n3 +2n2+5
k=1 n=1 2
∞
n
∞ ∞ X n
X 3 X 35.
10. n2e−n 23. tan(1=n) n+1
n=1
n=1 n=1
∞
∞ n+1 ∞ X 1
11. X(−1) 24. X cos(n=2) 36. ln(n)
nln(n) n2 +4n n=2 (ln(n))
n=2 n=1
∞
∞ ∞ X√
X n n Xn! n n
12. (−1) 2 25. 2 37. ( 2−1)
n +25 en n=1
n=1 n=1
∞ n 2 ∞ 2 ∞
X3n Xn +1 X√
13. 26. 38. ( n 2 − 1)
n! 5n
n=1 n=1 n=1
no reviews yet
Please Login to review.