207x Filetype PDF File size 0.22 MB Source: www.mathspanda.com
www.mathspanda.com
Geometry of complex numbers
Starter 5 4 3 2
1. (Review of last lesson) Express x − x + x − x + x − 1 as the product of linear and
quadratic factors with integer coefficients.
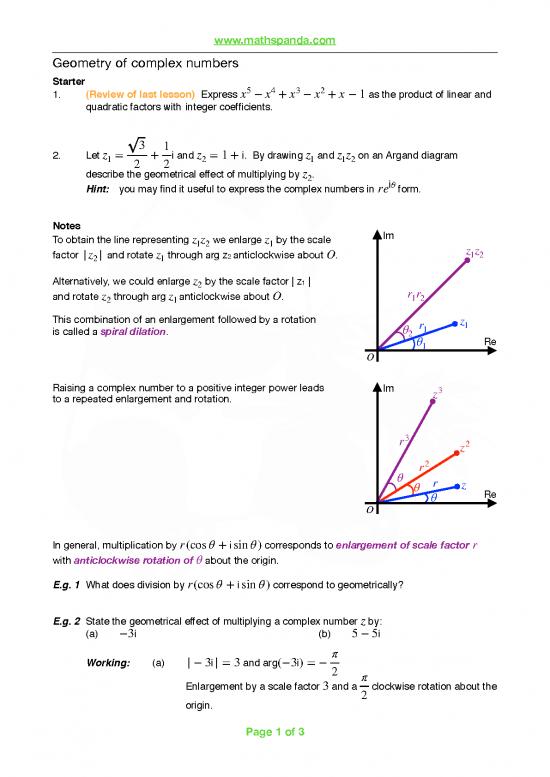
2. Let z = 3 + 1i and z = 1+i. By drawing z and z z on an Argand diagram
1 2 2 2 1 1 2
describe the geometrical effect of multiplying by z .
2 iθ
Hint: you may find it useful to express the complex numbers in re form.
Notes Im
To obtain the line representing z z we enlarge z by the scale
1 2 1 z z
factor |z | and rotate z through arg z anticlockwise about O.
1 2
2 1 2
Alternatively, we could enlarge z by the scale factor | z |
2 1 r r
and rotate z through arg z anticlockwise about O.
1 2
2 1
This combination of an enlargement followed by a rotation
z
r 1
is called a spiral dilation.
θ 1
2 θ Re
1
O
Raising a complex number to a positive integer power leads
Im z3
to a repeated enlargement and rotation.
r3 z2
r2
θ θ r z
θ Re
O
In general, multiplication by r(cosθ + isinθ) corresponds to enlargement of scale factor r
with anticlockwise rotation of θ about the origin.
E.g. 1 What does division by r(cosθ + isinθ) correspond to geometrically?
E.g. 2 State the geometrical effect of multiplying a complex number z by:
(a) −3i (b) 5−5i
Working: (a) | − 3i| = 3 and arg(−3i) = − π
2 π
Enlargement by a scale factor 3 and a 2 clockwise rotation about the
origin.
Page 1 of 3
www.mathspanda.com
E.g. 3 State the geometrical effect of dividing a complex number z by:
(a) 1+2i (b) −24−7i
| | 2 2 c
Working: (a) 1+2i = 1 +2 = 5 and arg(1+2i)=1.11
1 5 c
Enlargement by a scale factor 5 = 5 and a 1.11
clockwise rotation about the origin.
E.g. 4 Write down the complex w in the form a + ib such that the product wz represents the
following transformations of z: π
(a) an enlargement by scale factor 2 and a rotation of 3 anticlockwise about the origin.
(b) an enlargement by scale factor 1 and a rotation of 2π clockwise about the origin.
3 3
Working: (a) w =2 cos π +isin π =1+ 3i
( 3 3)
Alternatively:
Enlargement by scale factor 2: a2 +b2 = 2
a2 + b2 = 4
π −1 b π
Rotation of 3 anticlockwise about the origin: tan a = 3
b = 3
a
2 2 2 2 b = a 3
Substitute into a + b = 4: a +3a =4
Since angle is π anticlockwise: a = 1
3 b = 3
w =1+ 3i
E.g. 5 (a) Given the point representing a complex number z on an Argand diagram, explain
how to find the following points geometrically: 1
(i) 3z (ii) 2iz (iii) (3 + 2i)z
1 1 1
(b) Sketch an Argand diagram to represent the points O, 3z , 2iz and (3 + 2i)z and
state the geometrical connection between the points. 1 1 1
Video: Geometrical effects of conjugating a complex number
Explanation: Geometry of complex numbers
Video: Geometrical problem 1
Video: Geometrical problem 2
Solutions to Starter and E.g.s
Exercise
p49 2F Qu 1-14
Page 2 of 3
www.mathspanda.com
Summary
Multiplication by r(cosθ + isinθ) corresponds to enlargement of scale factor r with
anticlockwise rotation of θ about the origin.
Division by r(cosθ + isinθ) corresponds to enlargement of scale factor 1 with clockwise
r
rotation of θ about the origin.
Page 3 of 3
no reviews yet
Please Login to review.