200x Filetype PDF File size 0.15 MB Source: www.ccusd93.org
Big Ideas Math Geometry Chapter 3 Vocabulary
Study online at quizlet.com/_1r5juv
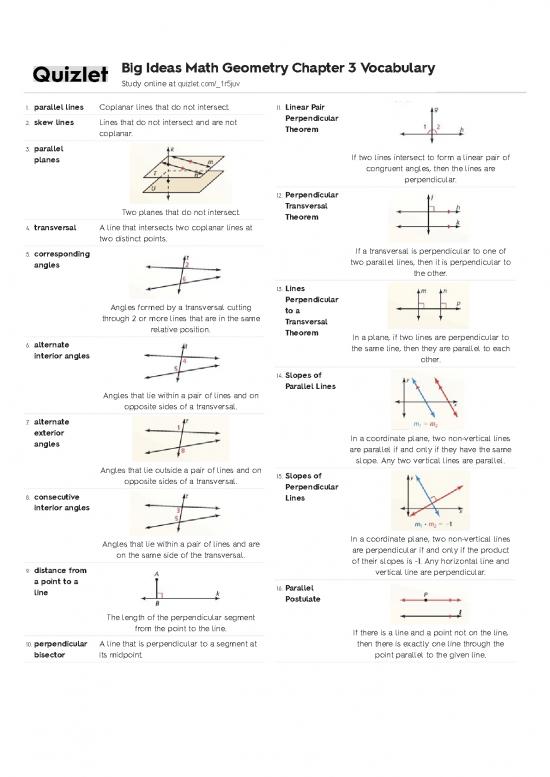
1. parallel lines Coplanar lines that do not intersect. 11. Linear Pair
Perpendicular
2. skew lines Lines that do not intersect and are not
Theorem
coplanar.
3. parallel
If two lines intersect to form a linear pair of
planes
congruent angles, then the lines are
perpendicular.
12. Perpendicular
Transversal
Two planes that do not intersect.
Theorem
4. transversal A line that intersects two coplanar lines at
two distinct points.
If a transversal is perpendicular to one of
5. corresponding
two parallel lines, then it is perpendicular to
angles
the other.
13. Lines
Perpendicular
Angles formed by a transversal cutting
to a
through 2 or more lines that are in the same
Transversal
relative position.
Theorem
In a plane, if two lines are perpendicular to
6. alternate
the same line, then they are parallel to each
interior angles
other.
14. Slopes of
Parallel Lines
Angles that lie within a pair of lines and on
opposite sides of a transversal.
7. alternate
exterior
In a coordinate plane, two non-vertical lines
angles
are parallel if and only if they have the same
slope. Any two vertical lines are parallel.
Angles that lie outside a pair of lines and on
15. Slopes of
opposite sides of a transversal.
Perpendicular
8. consecutive
Lines
interior angles
In a coordinate plane, two non-vertical lines
Angles that lie within a pair of lines and are
are perpendicular if and only if the product
on the same side of the transversal.
of their slopes is -1. Any horizontal line and
9. distance from
vertical line are perpendicular.
a point to a
16. Parallel
line
Postulate
The length of the perpendicular segment
from the point to the line.
If there is a line and a point not on the line,
10. perpendicular A line that is perpendicular to a segment at then there is exactly one line through the
bisector its midpoint. point parallel to the given line.
17. Perpendicular 25. Consecutive
Postulate Interior Angles
Converse
If there is a line and a point not on the line,
If two lines are cut by a transversal and
then there is exactly one line through the
consecutive interior angles are congruent,
point perpendicular to the given line.
then the lines are parallel.
18. Corresponding If two parallel lines are cut by a transversal,
26. Transitive
Angles then the pairs of corresponding angles are
Property of
Theorem congruent.
Parallel Lines
19. Alternate If two parallel lines are cut by a transversal,
Interior then the pairs of alternate interior angles
Angles are congruent.
If line l is parallel to line m and line m is
Theorem
parallel to line n, then line l is parallel to
20. Alternate If two parallel lines are cut by a transversal,
line n.
Exterior then the alternate exterior angles are
Angles congruent.
Theorem
21. Consecutive If two parallel lines are cut by a transversal,
Interior then each pair of consecutive interior
Angles angles is supplementary.
Theorem
22. Corresponding
Angles
Converse
If two lines are cut by a transversal and
corresponding angles are congruent, then
the lines are parallel.
23. Alternate
Interior
Angles
Converse
If two lines are cut by a transversal and
alternate interior angles are congruent, then
the lines are parallel.
24. Alternate
Exterior
Angles
Converse
If two lines are cut by a transversal and
alternate exterior angles are congruent,
then the lines are parallel.
no reviews yet
Please Login to review.