214x Filetype PDF File size 0.10 MB Source: www.bahria.edu.pk
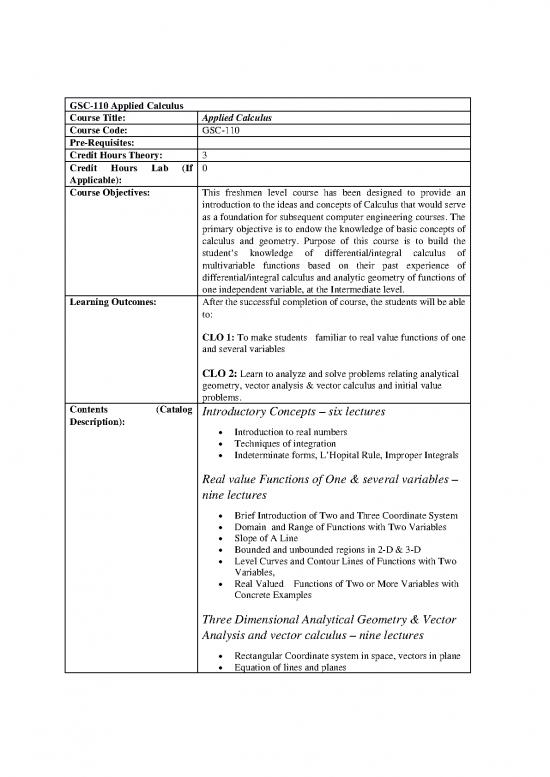
GSC-110 Applied Calculus
Course Title: Applied Calculus
Course Code: GSC-110
Pre-Requisites:
Credit Hours Theory: 3
0
Credit Hours Lab (If
Applicable):
Course Objectives: This freshmen level course has been designed to provide an
introduction to the ideas and concepts of Calculus that would serve
as a foundation for subsequent computer engineering courses. The
primary objective is to endow the knowledge of basic concepts of
calculus and geometry. Purpose of this course is to build the
student’s knowledge of differential/integral calculus of
multivariable functions based on their past experience of
differential/integral calculus and analytic geometry of functions of
one independent variable, at the Intermediate level.
Learning Outcomes: After the successful completion of course, the students will be able
to:
CLO 1: To make students familiar to real value functions of one
and several variables
CLO 2: Learn to analyze and solve problems relating analytical
geometry, vector analysis & vector calculus and initial value
problems.
Contents (Catalog
Description): Introductory Concepts – six lectures
Introduction to real numbers
Techniques of integration
Indeterminate forms, L’Hopital Rule, Improper Integrals
Real value Functions of One & several variables –
nine lectures
Brief Introduction of Two and Three Coordinate System
Domain and Range of Functions with Two Variables
Slope of A Line
Bounded and unbounded regions in 2-D & 3-D
Level Curves and Contour Lines of Functions with Two
Variables,
Real Valued Functions of Two or More Variables with
Concrete Examples
Three Dimensional Analytical Geometry & Vector
Analysis and vector calculus – nine lectures
Rectangular Coordinate system in space, vectors in plane
Equation of lines and planes
Norms, Direction Cosines, Dot and Cross products
Scalar & vector fields, gradient & directional derivatives
Cylindrical, spherical &p polar coordinates
Divergence and Curl of vector field(divergence & Stoke’s
theorem)
Infinite Sequence & series –six lectures
Introduction to series and sequences
Convergence & Divergence of infinite series
Integral test/limit comparison test/alternating series test
Ratio and root tests
Absolute Convergence & Divergence
Taylor & McLaurin series
Differential Calculus of Multivariable functions,
limits & Continuity – nine lectures
Functions of several variables
st nd
Partial derivatives (1 ,2 & higher order PDs of two/three
variables)
Chain rule
PD of Implicit functions
Linearization & Total differentials
Limits and continuity of function of several variables
Theorems on limits
Multiple Integrals – nine lectures
Introduction to Double & Triple Integrals
Double Integrals over Rectangular & non-rectangular
Regions
Fubini’s Theorem
Methods of calculating limits over non-rectangular
regions
Applications of double integrals
Triple Integrals (calculating area and volumes)
Applications of triple integrals
Line Integrals
Path independence
Recommended Text Books: Calculus and Analytical Geometry, 9th Ed. by George B. Thomas,
Jr. and Ross L. Finney
Reference Books: Calculus, 10th Edition by Anton, Bivens, Davis
Calculus and Analytical Geometry, 10th Ed. by George B.
Thomas, Jr. and Ross L. Finney
Helping Web Sites:
Attendance is mandatory. Every class is important. All deadlines
are hard. Under normal circumstances late work will not be
accepted. Students are required to take all the tests. No make-up
tests will be given under normal circumstances. There is 0 tolerance
for plagiarism. Any form of cheating on
exams/assignments/quizzes is subject to serious penalty.
Attendance
General Instructions for 75% attendance is mandatory. Latecomers will be marked as
students: absent.
Evaluation Criteria
Assignments/projects 20%
Quizzes 10%
Mid-Term 20%
Final 50%
CONTRIBUTION OF COURSE LEARNING OUTCOMES (CLOs) TO PROGRAMME
LEARNING OUTCOMES (PLOs)
BS Software Engineering Applied Calculus
No Program Learning Outcomes Course Learning Outcomes
12345
1 Engineering Knowledge
2 Problem analysis
3 Design/Development of solutions
4 Investigation
5 Modern tool usage
6 Engineer and society
7 Environment and sustainability
8 Ethics
9 Individual and Team work
10 Communication
11 Project Management
12 Lifelong learning
no reviews yet
Please Login to review.