222x Filetype PDF File size 0.68 MB Source: achieve.lausd.net
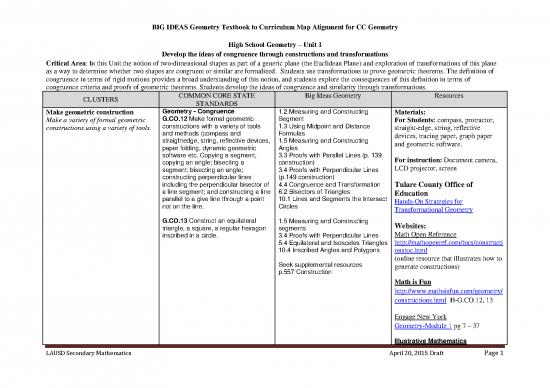
BIG IDEAS Geometry Textbook to Curriculum Map Alignment for CC Geometry
High School Geometry – Unit 1
Develop the ideas of congruence through constructions and transformations
Critical Area: In this Unit the notion of two-dimensional shapes as part of a generic plane (the Euclidean Plane) and exploration of transformations of this plane
as a way to determine whether two shapes are congruent or similar are formalized. Students use transformations to prove geometric theorems. The definition of
congruence in terms of rigid motions provides a broad understanding of this notion, and students explore the consequences of this definition in terms of
congruence criteria and proofs of geometric theorems. Students develop the ideas of congruence and similarity through transformations.
CLUSTERS COMMON CORE STATE Big Ideas Geometry Resources
STANDARDS
Make geometric construction Geometry - Congruence 1.2 Measuring and Constructing Materials:
Make a variety of formal geometric G.CO.12 Make formal geometric Segment For Students: compass, protractor,
constructions using a variety of tools. constructions with a variety of tools 1.3 Using Midpoint and Distance straight-edge, string, reflective
and methods (compass and Formulas devices, tracing paper, graph paper
straightedge, string, reflective devices, 1.5 Measuring and Constructing and geometric software.
paper folding, dynamic geometric Angles
software etc. Copying a segment, 3.3 Proofs with Parallel Lines (p. 139 For instruction: Document camera,
copying an angle; bisecting a construction) LCD projector, screen
segment; bisecting an angle; 3.4 Proofs with Perpendicular Lines
constructing perpendicular lines (p.149 construction)
including the perpendicular bisector of 4.4 Congruence and Transformation Tulare County Office of
a line segment; and constructing a line 6.2 Bisectors of Triangles Education
parallel to a give line through a point 10.1 Lines and Segments the Intersect Hands-On Strategies for
not on the line. Circles Transformational Geometry
G.CO.13 Construct an equilateral 1.5 Measuring and Constructing Websites:
triangle, a square, a regular hexagon segments Math Open Reference
inscribed in a circle. 3.4 Proofs with Perpendicular Lines http://mathopenref.com/tocs/constructi
5.4 Equilateral and Isosceles Triangles
10.4 Inscribed Angles and Polygons onstoc.html
(online resource that illustrates how to
Seek supplemental resources generate constructions)
p.557 Construction
Math is Fun
http://www.mathsisfun.com/geometry/
constructions.html H-G.CO.12, 13
Engage New York
Geometry-Module 1 pg 7 – 37
Illustrative Mathematics
LAUSD Secondary Mathematics April 20, 2015 Draft Page 1
BIG IDEAS Geometry Textbook to Curriculum Map Alignment for CC Geometry
CLUSTERS COMMON CORE STATE Big Ideas Geometry Resources
STANDARDS
Make Formal Constructions
More Constructions
Experiment with transformations in Geometry - Congruence 1.1 Points, Lines, and Planes Interactive
the plan G.CO.1 Know precise definitions of 1.2 Measuring and Constructing http://www.shodor.org/interactivate/act
angle, circle, perpendicular lines, Segments ivities/Transmographer/
Develop precise definitions of parallel lines, and line segment, based 1.3 Using Midpoint and Distance
geometric figures based on the on the undefined notions of point, line, Formulas Illustrative Mathematics
undefined notions of point, line, distance along a line, and distance 1.5 Measuring and Constructing Fixed Points of rigid Motion
distance along a line and distance around a circular arc. Angles Dilations and Distances
around a circular arc. 1.6 Describing Pairs of Angles Horizontal Stretch of Plane
2.5 Proving Statements about
Segments and Angles Mars Tasks:
Experiment with transformations in 2.6 Proving Geometric Relationships Aaron’s Designs
the plane. 3.1 Pairs of Lines and Angles Possible Triangle Constructions
10.1 Lines and Segments That Transforming 2D Figures
Intersect Circles
11.1 Circumference and Arc Length Mathematics Vision Project:
Module 6: Congruence, Constructions
G.CO.2 Represent transformations in 4.1 Translations and Proof
the plane using e.g. transparencies 4.2 Reflections
and geometry software; describe 4.3 Rotations Module 5: Geometric Figures
transformations as functions that take 4.5 Dilations
points in the plane as inputs and give Illuminations
other points as outputs. Compare
transformations that preserve distance Security Camera Placement
and angle to those that do not (e.g. Placing a Fire Hydrant
translation versus horizontal stretch.) Pizza Delivery Regions
Perplexing Parallelograms
G.CO.3 Given a rectangle, 4.2 Reflections
parallelogram, trapezoid, or regular 4.3 Rotations
polygon, describe the rotations and California Mathematics
reflections that carry it onto itself. Project
Transformational Geometry
G.CO.4 Develop definitions of 4.1 Translations
rotations, reflections, and translations 4.2 Reflections Teaching Channel
in terms of angles, circles 4.3 Rotations Collaborative Work with
perpendicular lines, parallel lines, and Transformations
line segments.
LAUSD Secondary Mathematics April 20, 2015 Draft Page 2
BIG IDEAS Geometry Textbook to Curriculum Map Alignment for CC Geometry
CLUSTERS COMMON CORE STATE Big Ideas Geometry Resources
STANDARDS
G.CO.5 Given a geometric figure and 4.1 Translations
a rotation, reflection or translation, 4.2 Reflections
draw the transformed figure using e.g. 4.3 Rotations
graph paper, tracing paper, or 4.4 Congruence and Transformations
geometry software. Specify a 4.6 Similarity and Transformations
sequence of transformations that will 5.3 Proving Triangle Congruence by
carry a given figure onto another. SAS
5.5 Proving Triangle Congruence by
SSS
5.6 Proving Triangle Congruence by
ASA and AAS
Understand congruence in terms of Geometry - Congruence Reflect on Background Knowledge Illustrative Mathematics
rigid motions Understand Congruence in terms of
G.CO.6 Use geometric descriptions of 4.1 Translations Rigid Motion
Use rigid motion to map rigid motions to transform figures and 4.2 Reflections
corresponding parts of congruent to predict the effect of a given rigid 4.3 Rotations Is this a rectangle?
triangle onto each other. motion on a given figure; given two 4.4 Congruence and Transformations
figures, use the definition of Illuminations
Explain triangle congruence in terms congruence in terms of rigid motions
of rigid motions. to decide if they are congruent. Triangle Classification
G.CO.7 Use definition of congruence 5.2 Congruent Polygons Teaching Channel
in terms of rigid motions to show that Formative Assessment: Understanding
two triangles are congruent if and only Congruence
if corresponding pairs of sides and
corresponding pairs of angles are
congruent.
G.CO.8 Explain how the criteria for 5.3 Proving Triangle Congruence by
triangle congruence (ASA, SAS, and SAS
SSS) follow the definition of 5.5 Proving Triangle Congruence by
congruence in terms of rigid motions. SSS
5.6 Proving Triangle Congruence by
ASA and AAS
Prove geometric theorems Geometry - Congruence 2.5 Illustrative Mathematics
Prove theorems about lines and angles, G.CO.9 Prove theorems about lines 2.6 https://www.illustrativemathematics.or
LAUSD Secondary Mathematics April 20, 2015 Draft Page 3
BIG IDEAS Geometry Textbook to Curriculum Map Alignment for CC Geometry
CLUSTERS COMMON CORE STATE Big Ideas Geometry Resources
STANDARDS
triangles; and parallelograms. and angles. Theorems include: vertical 3.2 Parallel Lines and Transversals g/content-standards/HSG/CO/B
angles are congruent; when a 3.3 Proofs with Parallel Lines
transversal crosses parallel lines, 3.4 Proofs with Perpendicular Lines Mars Task:
alternate interior angles are congruent 4.1 Translations
and corresponding angles are 6.1 Perpendicular and Angle Bisectors Evaluating Statements About
congruent; points on a perpendicular Length and Area
bisector of a line segment are exactly
Illuminations:
those equidistant from the segment’s
endpoints. Perplexing Parallelograms
G.CO.10 Prove theorems about 5.1 Angles of Triangles
triangles. Theorems include: 5.4 Equilateral and Isosceles Triangle
measures of interior angles of a 6.2 Bisectors of Triangles
triangle sum to 180°; base angles of 6.3 Medians and Altitudes of Triangles
isosceles triangles are congruent; the 6.4 The Triangle Midsegment
segment joining midpoints of two Theorem
sides of a triangle is parallel to the 6.5 Indirect Proof and Inequalities in
third side and half the length; the One Triangles
medians of a triangle meet at a point. (Paul and Oksana include task p.346)
6.6 Inequalities in Two Triangles
G.CO.11 Prove theorems about 7.2 Properties of Parallelograms
parallelograms. Theorems include: 7.3 Proving that a Quadrilateral is a
opposite sides are congruent, opposite Parallelogram
angles are congruent; the diagonals of 7.4 Properties of Special
a parallelogram bisect each other, and Parallelograms
conversely, rectangles are
parallelograms with congruent
diagonals.
LAUSD Secondary Mathematics April 20, 2015 Draft Page 4
no reviews yet
Please Login to review.